Twenty-four, Forty-two, and I Love You. Keeping It Complex
Abstract
"In this classic article, Duckworth focuses on the nature of understanding by leading the reader through the process of extended clinical interviewing. Duckworth describes some of her own explorations of science and how those experiences showed her what learning could be like. Those experiences included working with 'a highly imaginative bunch of scientists and teachers of science' while developing the Elementary Science Study, a curriculum development program."
Eleanor Duckworth, "Twenty-four, Forty-two, and I Love You: Keeping It Complex,"
Harvard Educational Review, 61:1 (February, 1991), pp. 1-24. Copyright (c) 1991 by the President and Fellows of Harvard College. All rights reserved. Used with permission.
In this article, Eleanor Duckworth focuses on the nature of understanding by leading the reader through the process of extended clinical interviewing. Duckworth describes some of her own explorations of science and how those experiences showed her what learning could be like. Those experiences included working with "a highly imaginative bunch of scientists and teachers of science" while developing the Elementary Science Study, a curriculum development program. As she describes it, Duckworth 'got hooked" on the excitement of learning and has been an educator ever since, working to develop engaging learning experiences for both teachers and students. This article continues her effort to do just that, with lengthy descriptions of her own and her students' struggles--and enjoyment--as they attempt to understand and define various phenomena. And with that, she opens the discussion of "keeping it complex."
In my entire life as a student, I remember only twice being given the opportunity to come up with my own ideas, a fact I consider typical and terrible. I would like to start this article by telling how I came to realize that schooling could be different from what I had experienced.
Figuring Out My Own Ideas
After my university studies, I joined the Elementary Science Study, a curriculum development program. I had been hired because of my background with Piaget, studying how science and math ideas develop in children, and had no formal training in either education or science. While the first of these lacks was probably a liability, the second turned out to be a great boon. I was working with a highly imaginative bunch of scientists and teachers of science, all trying to put together their favorite kinds of experience to entice children. Because I was innocent in science I made a great "sample child" for my colleagues, and I spent a lot of time exploring the materials and the issues that they came up with. Of the many areas I explored, three seemingly unrelated ones came together in a way that showed me what learning could be like. I got hooked and have been an educator ever since, trying to develop learning experiences of that sort for every child and every teacher. It was the first time--with two exceptions mentioned in the opening sentence--that I got excited about my own ideas. I had been excited about ideas before, but they had always been somebody else's ideas. My struggle had always been to get in on what I thought somebody else knew and knew to be important. This was the first time that I had a sense of what it was like to pay attention to my own ideas.
It is, of course, exhilarating to find that your own ideas can lead you some where. Few feelings are likely to be more effective in getting you to keep on think ing about things on your own. I would like to focus here, though, not so much on my feelings as on the nature of my understanding.
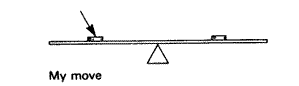
One team of colleagues was developing ways to study balances. They posed problems with a simple balance that consisted of a strip of pegboard resting on a rounded support with metal washers as weights. In each case, they started with the balance in equilibrium, horizontal. Then, holding the balance, they moved one or more weights and asked me to adjust other weights so that when they let go, the balance arm would remain horizontal (see Elementary Science Study, 1967b).
For example, they set up a relatively easy problem with the balance, as shown here:

Where could I add one washer, so the board would stay balanced? My solution was as follows:
They then gave me a problem that I found more difficult: they presented me with the board balanced with one washer on one side and two washers stacked on the other side, but closer to the middle. If they moved the single washer a certain distance to the right, how could I move just one of the other two washers, so the board would still balance?

I found that this solution worked:
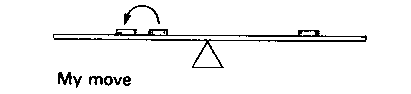
Through this example and others similar to it, I found that it did not seem to matter where the washers started; I just had to move one of them the same distance the original had been moved on the other side, but in the opposite direction.
My grand triumph was the following problem. To start with, they put three washers in a pile on one side so as to balance one on the other:
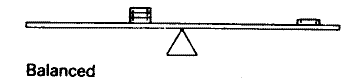
Then they moved the single one a long way--practically to the center. Again, how could I move just one of the others so it would still balance?
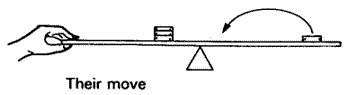
Well, I knew by now that I should try to move it just as far in the opposite direction, but there was no room. I ran into the middle almost right away. So what should I do? Move it in the same direction? That didn't seem right. Move it as far as I could towards the middle--just barely short of the middle? I thought I might try that. But the one I decided to try was my first idea--moving the washer in the opposite direction, even though it meant crossing the middle.
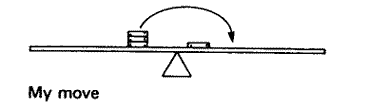
It felt to me like a very daring move And it worked! The rule worked, even across the middle. I remember saying to my colleagues at the time that I felt like Helen Keller.
I did not stop then. Among other things, I tried designing balances myself, and eventually even figured out what the differences were between a balance and a see saw that accounted for the fact that the balance with nothing on it is horizontal, while a seesaw with nobody on it always has one end up in the air.
A second group was working on a study of what they called Gases and "Airs" (Elementary Science Study, 1967a). The tight sequence of reasoning demanded by this unit turned out not to work very well with elementary school children, but the unit did entail a wonderful variety of experiences that, for me, gave substance to what gases and airs are. It started from a close and critical look at the classic school science lab demonstration of burning a candle in a tube inverted over water: the water rises, the candle goes out, and one has "proven" that the atmosphere is 20 percent oxygen. But, there are some problems, as my colleagues pointed out. For one thing, the water doesn't rise gradually as the candle burns; it rises suddenly after the flame is out. If it were gradually using up the oxygen, wouldn't it gradually rise? Another problem: the amount that it rises may indeed average about 20 percent, but it varies widely; in contrast, when wet steel wool is wedged into a tube above water and left to rust overnight, the water rises exactly the same amount in each tube.

| Water rise after 4 candles burned | Water rise with steelwool overnight |
I became very good at putting into a tube whatever kind of air I wanted to. Using a syringe, I could take air from any tube and put it into another tube that had no air in it (by virtue of being full of water). Bubbles came to be real things filled with some one kind of air--room air, lung air, steel wool air, or other. Putting an Alka Seltzer tablet under the lip of a water-filled tube, for example, did this:

and I had a tube full of Alka Seltzer air.
I came to imagine the inverse of filing any container with liquid. As long as your container has no other liquid in it already, you can put it straight under the dripping liquid, and you'll capture all that is falling right over the opening In the inverse, as in the case of some escaping Alka Seltzer air, you could think of it this way:
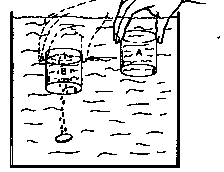
In a bucket of water, move a water-filled jar over the bubbles, and you will collect the escaping Alka Seltzer air.
This is not, I hasten to point out, intended as a practical example: I've never happened to be holding a water-filled jar upside down in a bucket of water- when an Alka Seltzer tablet dropped into the bucket. But conceptually it helped me a lot: an "air" was for me as real as a liquid.
A third area that I explored originated in my attempts to build on my Piaget background. I thought of trying to find some situations for young children in which a certain order was maintained in spite of some striking change. It occurred to me to use the constant ordering of liquids floating on each other in a tube. Though the idea had less mileage in it for little children than I had thought it might, it did have some value (see Duckworth, 1964). More importantly for my education, however, it led me into a long series of explorations with liquids, starting with trying to make as many floating layers as I could in one tube. If I did not shake the tube, I could manage about six layers, and I experimented with dyes to keep the layers distinguishable. I expanded my horizons to include solid pieces -seeds, bits of plastic, bits of wood, bits of food. I don't recall any of these specifics, but a radish seed, say, would fall through three layers and sit on the fourth--and every radish seed would do that. One kind of plastic would sit on the second layer, another kind would fall through four, and so on. Some material (I do not now remember what, and it took me a long time to find this material) stopped at the top of the top surface and floated there.
I also tried to mix alcohol and water so that the resulting liquid would have exactly the same density as the salad oil I was working with--to see what would happen when neither liquid would necessarily float on top of the other. Would I be able to make stripes with them? Or would they stand side by side, with a vertical separation? Or what? I found that the oil always formed itself into a single enor mous sphere in the middle of the water-alcohol liquid; and that this sphere always moved slowly either to the top or to the bottom of the water-alcohol liquid. No matter how delicately I added one drop of wafer or of alcohol, I could never get the sphere of oil to float right in the middle--it was always either just heavier or just lighter. (These explorations came back in my own teaching more than ten years later; see Duckworth, 1986.)
Six or eight months after I started learning science like this, someone presented a puzzle that happened to draw on the three areas I had been exploring. I think I was the only person around at the time who put together the right prediction.
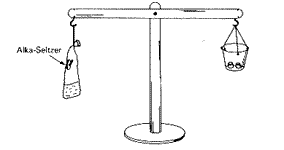
On the left-hand side of this balance is a plastic bag sealed airtight; an Alka Seltzer tablet is stuck in a piece of plasticene near the top, and some water is in the bottom. On the right-hand side is just enough weight to balance the arm. The question is, what will happen to the balance of the arm if the bag is shaken, and the tablet falls into the water?
Most of the people present knew that when the tablet fell into the water, a lot of "Alka Seltzer air" would be formed and the bag would fill out. Some people thought that the arm would remain level, because the same matter that was in the bag to start with was still in it at the end, even if in a different form, so the weight would not change at all. Others thought that the left side would go down, because Alka Seltzer air (being, as they knew, carbon dioxide) is heavier than room air. My prediction, which, in fact, turned out to be the case, was that the left side would go up, because the filled-out bag would take up more space, while adding no more weight, thus being more buoyant in the surrounding sea of air.
I believe that it was because I started from my own ideas and found my own ways into these parts of the world that my understanding of balances, "airs," and floating belonged so thoroughly to me. Notice the difference between what usually happens in formal education--presenting the simplest, neatest explanation of "the law of moments," "the composition of the atmosphere," "density," "buoyancy," or whatever; and my experience of being enticed with the funny, frustrating, intriguing, unpredictable complexities of the world around me. Instead of disassociating myself from my own interests in my struggle to find out what whoever was supposed to "know" might have understood by the word "buoyancy," my learning was based on my own connections, within the idiosyncrasies of my own system of thoughts. The very complexities of the subject matters enabled me to connect with them, made them accessible, and the integrity of my own ideas enabled me to retrieve those connections when they could help me understand a new situation.
Lisa Schneier (1990) describes the relationship between complexity and accessibility in this way:
[W]e organize subject matter into a neat series of steps which assumes a profound uniformity among students. We sand away at the interesting edges of subject matter until it is so free from its natural complexities, so neat, that there is not a crevice left as an opening. All that is left is to hand it to them, scrubbed and smooth, so that they can view it as outsiders. (p. 4)
The experience of my science explorations was the exact opposite.
The Universe in a Sentence
My favorite radio show is "A Hitchhiker's Guide to the Galaxy." In one episode, a computer is built expressly for the purpose of answering the question, "What is the meaning of life, the universe, and everything?" When it is ready, they ask it if it can answer that question. It says, yes, it can, but that it will take, as I recall, seven million years. They say, "Well, OK, go to it." Seven million years later, whoever is around goes to learn the answer. The computer says that it does have the answer, but that it might be a little disappointing. "No, no," they say, "go ahead, what is it?" "Forty-two," the computer says.
Who knows? Maybe forty-two is the answer. But such an answer is of no more help to us than no answer at all. It does not speak to our level of interaction with the mysteries of our existence.
Note the parallels with the following story from Lisa Schneier's class in an urban high school:
It had been a lively class, with the various Juliets taking turns standing on a table and the Romeos making elaborate and often comical gestures as they stood below. . . . A group of ninth graders and I were working on a scene from Romeo and Juliet.They had chosen to read the balcony scene aloud and were acting it out, taking turns with the parts. They took the difficult language and its foreign style into stride, at times staying true to the text and at others replacing or skipping words and phrases. It was clear as they spoke that at points the words held meaning for them and at others they hadn't a clue as to what it was that they were reading. But we didn't stop much for discussion; the students were enjoying this kind of involvement with each other, and there was a momentum in the reading that I didn't want to interrupt.But our last Romeo of the day finally did interrupt it. We had started the scene again to give more readers a turn, and he had begun to wade through his first speech. In the midst of it, he broke off, shook his head impatiently, and turned to me. "He loves her. That's what he's saying. So why all that other stuff? Why not just say it? I love you! (to the current Juliet). There!" And then in a memorable tone, a mixture of humor, frustration, and holiest confusion: "Why can't he just say what he means?" (Schneier, 1990, pp. 1-2)
Why doesn't Shakespeare just say what he means? Of course that's what he is doing: "what he means" is complex. The words he chooses are the best he can choose to say what he wants to say. Poems and stories and paintings and dance and music are not just fancy ways of saying what could be said in a sentence. "I love you" does not quite express everything that Shakespeare meant, just as "forty-two" does not quite substitute for living our lives. There is a parallel here between a poet and a teacher: the universe is complex; science is complex; the poet's thoughts and feelings are complex "Forty-two" doesn't do the trick. Neither does "buoyancy." Nor, in this case, does "I love you."
In this spirit, when studying a poem with a class, I start by asking students what they notice--an invitation to keep every complexity of the poem under consideration. People notice very different things, and almost each thing noticed leads to a question or another thought. Putting together what everyone notices and returning to the poem to try to look for answers to the questions leads to an understanding of the poem that is greatly expanded for each of us. Take, for instance, this Frost poem:
DESIGN
I found a dimpled spider, fat and white,
On a white heal-all, holding up a moth
Like a white piece of rigid satin cloth--
Assorted characters of death and blight
Mixed ready to begin the morning right,
Like the ingredients of a witches' broth--
A snow-drop spider, a flower like froth,
And dead wings carried like a paper kite.
What had that flower to do with being white,
The wayside blue and innocent heal-all?
What brought the kindred spider to that height,
Then steered the white moth thither in the night?
What but design of darkness to appall?--
If design govern in a thing so small.1
Somebody will notice that there is a lot of white. Somebody will mention the rhyme scheme, or will imitate the rhythm. Somebody will mention that the first part of the poem seems to present a picture, and the second half seems to ask questions about it. Different people point out different possible plays on words: kindred and dreadful kin; appall and a funeral pall; a paper kite and a bird kite; morning right and morning rite; morning and mourning. Different people have different thoughts about whether the darkness is that which appalls, or that which is appalled. Arguments develop about why the flower is described as white in the first line, and blue in the ninth. This is a bare beginning. A group of adults can easily go for more than an hour with increasing interest, and everybody's initial understanding is expanded by hearing from others.2
I have always been frightened by being asked: "What is the meaning of this poem?" My reaction is, "How could I know? I'm no good with poems!" But it is easy for me to point out something that I notice about it, and in turn to listen to what other people notice, about it, and to figure out whether I think that what they say makes sense, and why, and what other thoughts their ideas provoke in me. Many students have feelings similar to these. One in particular said that she had determined when we started discussing the poem that she would not say a word, knowing nothing about poems and feeling scared by them. But as she heard the various things that people were saying, her own thoughts developed, and she finally couldn't contain herself, so much did she have to say and so strongly did she feel about it. One student referred to himself as a "poem-phobe," which prompted another student to say, "If Frost had been able to put what he had to say into a sentence, he would have. So don't worry that you can't."
I recognized that this was the same thought I had about the accessibility of science. It is in acknowledging the complexity of the poem, not "sand[ing] away at the interesting edges," to use Schneier's words, that we render it accessible. Our understanding seeks to do justice to the complexity that the poet sought to render, and by the same token it belongs to us. Just as the poet seeks to present his thoughts and feelings in all their complexity, and in so doing opens a multiplicity of paths into his meaning, likewise a teacher who presents a subject matter in all its complexity makes it more accessible by opening a multiplicity of paths into it.
"I Know There Are Twenty-four"
I ask students to do the following: Take a fistful of four different kinds of markers (four colors of paper clips or four kinds of dried beans, for example) to represent four children who are going to the movies. Lay out the different arrangements in which they can sit in four adjacent seats. Some students ask, "Do I really have to do this? I know there are twenty-four." And I say, yes, you really have to; the question isn't how many arrangements, the question is what are the arrangements--each of them. (It happens, not infrequently, that someone who has impatiently affirmed that there will be twenty-four, because he or she knows a formula, has trouble generating the actual arrangements--which strikes me as not too different from knowing that the meaning of life is forty-two.) And the question behind that is, when you think you have laid out all the arrangements, how could you convince yourself or anybody else that you don't have any repeats, and that you are not missing any? I urge the reader to try this before continuing, and to see what system she or he comes up with.
Most non-math people start this exercise more or less randomly, but many systems emerge when they think about whether they have generated all the possible arrangements. In what follows I will present some of these systems.
Some people make diagonals, such as with the P in the following arrangements:
PBLM
MPBL
LMPB
BLMP
This could be called the 'revolving" system, where the last letter to the right revolves around to appear on the left, and everything moves over one. This looks systematic and promising, but when they follow this rule to the fifth step, it turns out to be a repeat of the first (PBLM). So they have to side-step, and think about how to find the various different possible starting points.
Another system which keeps P on the diagonal is the "squeeze between" system:
PBLM
BPLM
BLPM
BLMP
Move P to the right by squeezing it in between the next two letters. Again, the question arises about what to do after the fourth.
You could reinterpret that system to be not "squeeze between" but "exchange": Keep P moving on the diagonal by exchanging it with whatever letter is in the place where it will be moving. That explains the four above, and allows you to keep going:
PLMB
LPMB
LMPB
LMBP
PMBL
MPBL
MBPL
MBLP
At this point, after twelve arrangements, we get back to the starting point. Is that, then, all there are? Is there a reason to think that this system would have generated all we could possibly get? Is there a reason to think it is inadequate? Or can't we tell anything about it at all?
Not all approaches use diagonals. For the next ones I will limit the discussion to three children in three seats in order to write out fewer arrangements.
Many people, as a system starts to emerge, lay out something like this:
LMB
LBM
MLB
By this time they have an idea about what they will put next, and most think that their idea is the only sensible, systematic possibility. The first surprise is that there are two different, almost equally popular, next moves:
MBL or BLM
And the two completed lists would look like this:
I
LMB
LBM
MLB
MBL
BLM
BML
II
LMB
LBM
MLH
HLM
MBL
BML
The system on the left started with two L's in the first position, then put two M's in the first position, and then two B's The system on the right started with the L's in the first position, then moved the L's to the second position, and then to the last position. In both cases, people can say, "Once I have one position filled, there are only two ways to fill the other two, so these are the only possible six ways for three children to sit." They are two very different systems, and yet they could up with the same exact arrangements.
Playing this out with four children and four seats, using, for example, system 1, would give this result:
PLMB
PLBM
PMLB
PMBL
PBLM
PBML
There would be six different arrangements with P in the first position. There would, therefore, be six ways to put each of the four letters in the first position; that is, four times six ways altogether. (Playing out system II above, P would end up in each position six times--again, four times six ways altogether.)
One nine-year-old--no math whiz, he--after placing a few arrangements according to no system that I could see, started to make new ones by reversing pairs in the ones he already had. (From PLBM, say, he might make PBLM; or from MLPB he might make LMPB.) He worked slowly, and for a long time he would make a new arrangement and then check to see whether he already had it rather than generate a new one from some overall system he had in his mind. After a long time, though (he worked at this for close to an hour), and as he explained to me what he was doing, a system emerged; he started to know how to look for ones that were missing and to fill in the gaps. It was a system that was totally new to me. He never articulated it as clearly as I am about to here, but essentially his system was as follows.
Start with one block, let's say P, and pair it up with each of the other blocks in turn. Let's start with the pair PL; put them in the middle, and put the two remaining blocks at either end. Then reverse the two on the ends. Then reverse the originals (PL becomes LP) and repeat. Then put the end-ones in the middle and the middle-ones at the ends and start over.
BPLM
MPLB
BLPM
MLPB
PBML
LBMP
PMBL
LMBP
Now we have eight. Starting with PM gives us another eight and starting with PB gives us eight more. This way you get three times eight instead of four times six. Is there any reason that this system is a convincing one? When you've started with P and each of the other letters and done all the rearrangements as described, is there any reason to think that you would necessarily hit all the possibilities?
I could go on. Looking for relationships among the systems enhances our understanding even more: What is the relationship between a system that has four variations of six positions and a system that has three variations of eight positions? The point is that the more you look at this question, the more ways there are to see it. "Twenty-four" is a sadly impoverished version of all that can be understood about it. Just as with the poem, each different way of thinking about it illuminates all of the others--a wonderful pay-off for allowing for the complexities of the matter. Note that in this math problem, as with the poem, individuals tend to think that their way is the one way to look at it, unless they are in a social context where other possibilities are presented; then it is not a matter of replacing their point of view, but of enhancing it.
Of course, many people raise for themselves the question of arrangements of five children, and work out a formula that applies to any number--a formula which, then, represents their understanding instead of substituting for it.
One further comment: Another nine-year-old pointed out to me that, once he had laid out all the arrangements (and he came up with twenty-four), if he removed the first item from all of them, the twenty-four arrangements of three items are still all different from each other. After some thought, I can more or less understand that this must be so. But it certainly brought me up short when he raised the idea.
